← back

The Second Derivative

by ongzz(3 minute read · 0 views)

the derivative

when i first learned calculus, i was taught how to take functions' derivatives, and to set them equal to zero to find their turning points. i was BLOWN away by this, thinking to myself why it wasn't taught earlier on.

looking back, i think the reason i felt like this was because we were always asked to find the turning point of a parabola, something like $f(x) = 3x^2-12x+16$ by completing the square and writing it in vertex form (which looks like $f(x)=a(x-h)^2+k$).

i didn't really like it - at the time, we were taught how to "completing the square", butweren't told the "why" - i remember feeling super puzzled about why we had to divide by 2 before putting it into parentheses, so each time i did it i felt even more weirded out, like there's some hidden truth (eventually i figured it out though - just expand compare the coefficients of $(x-h)^2+k$ and $x^2+bx+c$ and solve for $h$)

going back to derivatives - the process felt magical. even with only the power rule, i could now solve for turning points very easily, but setting the derivative equal to $0$.

play around with it here! (remember - derivative of $f$ at $x$ $=$ slope of the tangent line at $x$, and slope = 0 at turning point)

but derivatives are not what this blog is about lmao

the second derivative test

shortly after learning that, we were taught second derivatives, taking the derivative of a derivative, derivative-ception. putting it in practice, it would look like

apparently by doing this, we could know whether or not the function is minimum or maximum just by doing math, without drawing graphs whatsoever!

determining a function's nature still felt a bit off, though - it didn't click for me instantly back then.

we were asked to remember that if $f''(x)>0$, the point would be a minimum; and if $f''(x)<0$, the point would be a maximum. isn't it weird though? maximum point implying a negative second derivative??

the way most people explain it is to think of the slope around that turning point - for a maximum turning point, the slope keeps decreasing, from positive slope, to 0 slope, to negative slope.

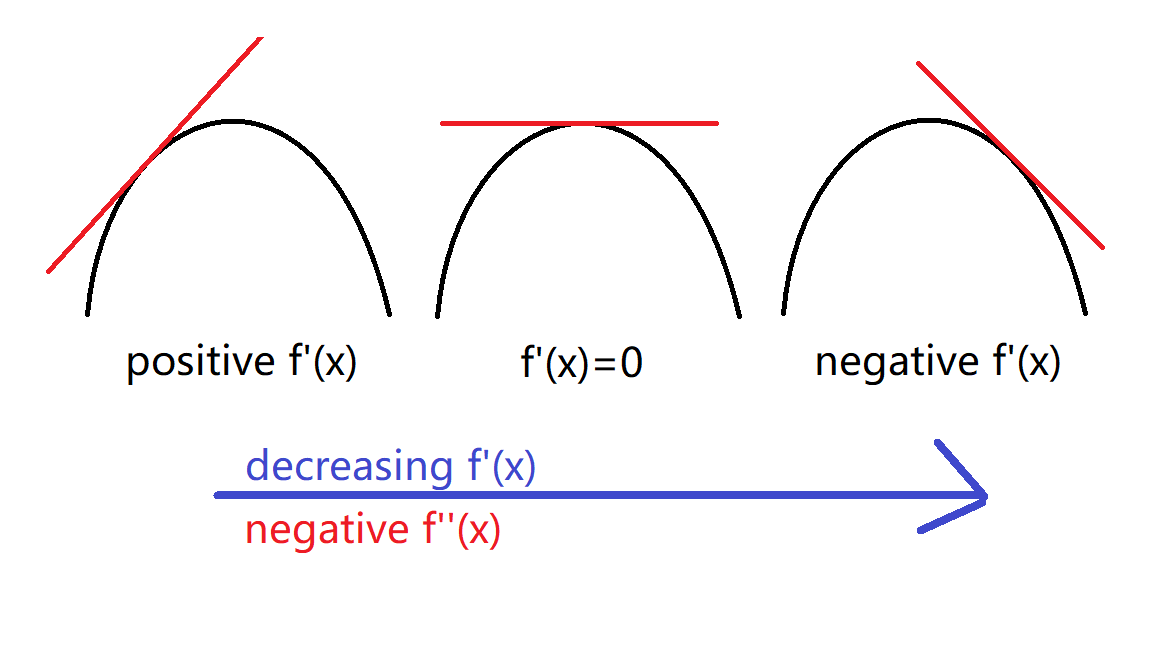
the same logic could be applied to a minimum point. so, because the 2nd derivative is the rate of change of the derivative, it would be negative at the maximum and positive at the minimum.

another perspective

the way i got around memorising this was thinking of it as a "force" - positive $f''(x)$ means there's a force "pulling" the graph upwards, and negative $f''(x)$ means there's a force "pulling" the graph downwards.

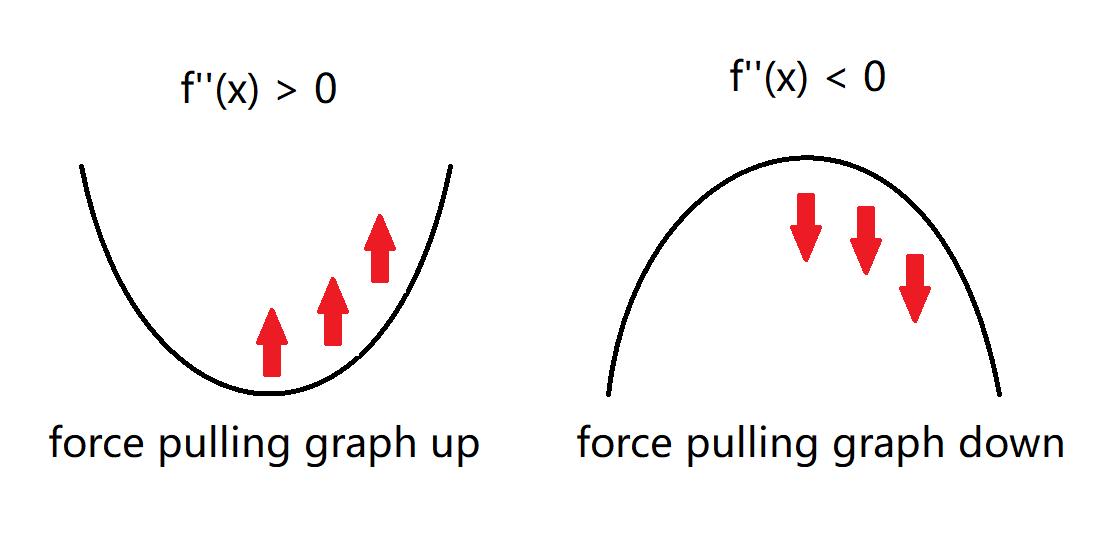
i'm not sure if this is a correct justification, but because $F=ma$ and $a=\frac{d^2}{dt^2}s$, the rate of change of the rate of change of displacement is acceleration, which is just force scaled by $\frac{1}{m}$. ($a=\frac{F}{m}$)

in our case, the 2nd derivative would be analagous to $F$orce and the $x$-axis as time, with the graph representing displacement over time.

conclusion

• maximum: $f'(x) = 0, f''(x) < 0$
• minimum: $f'(x) = 0, f''(x) > 0$
• how to memorise? forces!

thanks for reading, hope this helps anyone that reads this :P